# Achieving superhuman performance in the board game Squadro using AlphaZero on a single computer with no GPU
AlphaZero is an algorithm created by Deepmind (a company owned by Google) that showed impressive performance in multiple games. Their work became popular through the game of Go, as they have beaten the #1 world champion with very unconventional plays. This feat is particularly meaningful to me, as it was one of the events that led me to choose my major in Artificial Intelligence.
To achieve such results [1] [2], AlphaZero was trained 40 hours using 5000 first-generation TPUs and 64 second-generation TPUs. This computing power is still inaccessible to most companies today. Many researchers have worked on implementing AlphaZero in order to reproduce their feat on Go, chess or shōgi. Here are some popular implementations: ELF [3], Leela Zero [4], KataGo [5], AZFour [6]... Few implementations focus on a modest usage of computing resources, and none of them try to tackle games that are not solvable with exact algorithms.
The goal of my work was to replicate the algorithm starting from the official publications and apply it to a moderately complex board game, Squadro, using a single computer with no GPU. In this publication, I first explain how AlphaZero works, tune its hyperparameters, discuss the different challenges I have faced, and finally, I detail the learning process and my results.
# Methods
# Monte Carlo tree search
A Monte Carlo tree search (MCTS) is a tree where each node corresponds to a board game. The root of the tree is the current state of the board, and the goal is to search for the best action in order to win. Intuitively, an MCTS agent will estimate the probability of winning for each possible action and decide accordingly which one to play. To do that, the algorithm consists of 4 different steps: selection, expansion, simulation and backpropagation.
# Selection
Go down the tree in a best-first search fashion, until you reach a leaf node. Select nodes based on their UCT score:
The first term of the addition is referred as the exploitation term, while the second term is the exploration term. The exploitation term takes advantage of the moves it knows are great, meanwhile the exploration term tends to favor unvisited nodes. In theory, the exploration parameter should be equal to
# Expansion
If the selected node does not correspond to an end of the game, add the successors of this node to the tree. They correspond to the legal moves from the selected game board.
# Simulation
From the selected node, play randomly until you reach a game end (win/loss/draw).
# Backpropagation
Push the outcome of the game up in the tree: add it to the
Of course, you have to repeat this process several thousands of times in order to get precise results. Depending on the complexity of the game, this technique may already be sufficient to obtain decent performance. The biggest downside about this algorithm is that it must do a huge number of rollouts in order to play accurately. Imagine deriving the true winning probability in the game of Go (19x19 board) with a best-first search strategy... it would simply be computationally too huge!
# Algorithm 1 - Monte Carlo search tree
import math
# The "Node" class is voluntarily omitted, it is really
# straightforward to implement and does not add information
# for your understanding of the algorithm.
class MCTSAgent:
"""
Constructor for a Monte Carlo tree search agent.
@param rollouts: number of rollouts to make at each turn
@param c: exploration parameter
"""
def __init__(self, rollouts, c=1.4):
self.rollouts = rollouts
self.c = c
self.root = None
"""
Play an action for the current state, given the last action played.
@param state: current state of the game
@param last_action: last action played
@return: selected action
"""
def play(self, state, last_action):
# find root node for the search
if self.root is None:
self.root = Node(state.copy(), last_action)
else:
self.root = self.root.children[last_action]
# apply rollouts
for _ in range(self.rollouts):
self._rollout(self.root)
# play the most visited child
max_node = max(self.root.children, key=lambda n: n.N)
# reflect our action in the search tree
self.root = self.root.children[max_node.last_action]
return max_node.last_action
"""
Apply one rollout. It consists in four different steps:
- selection
- expansion
- simulation
- backpropagation
@param node: root node from where to apply the rollout
"""
def _rollout(self, node):
path = self._selection(node)
leaf = path[-1]
self._expansion(leaf)
reward = self._simulation(leaf)
self._backpropagation(path, reward)
"""
Go down the tree and select the first leaf node it encounters.
@param node: node from where to apply the selection phase
@return: path from `node` to the selected leaf node
"""
def _selection(self, node):
path = []
while True:
path.append(node)
if not node.is_expanded() or node.is_terminal():
return path
node = self._uct_select(node)
"""
Select one children based on their UCT score.
@param node: parent node
@return: selected children node
"""
def _uct_select(self, node):
def uct(n):
if n.N == 0:
# unvisited children have the highest priority
return float("inf")
return n.W / n.N + self.c * math.sqrt(math.log(node.N) / n.N)
return max(node.children, key=uct)
"""
Expand the given `node`.
@param node: node to expand
"""
def _expansion(self, node):
if node.is_expanded():
# already expanded
return
node.expand()
"""
Play the game until a terminal node is reached.
@param node: node from where to play
@return: outcome of the game (reward)
"""
def _simulation(self, node):
invert_reward = True
while True:
if node.is_terminal():
reward = node.reward()
return -reward if invert_reward else reward
node = node.get_random_child()
invert_reward = not invert_reward
"""
Backpropagrate the outcome of the game through the selected path.
@param path: selected path
@param reward: outcome of the game
"""
def _backpropagation(self, path, reward):
for node in reversed(path):
node.N += 1
node.W += reward
reward = 1.0 - reward
# AlphaZero
# Modified Monte Carlo tree search
The idea behind AlphaZero is to use a modified Monte Carlo tree search and to link it to a neural network such that it replaces the simulation phase. Indeed, the neural network will predict:
- A value ("reward") of the given state. It corresponds to the estimated probability of winning for the current player. It takes a value in the range
- A policy vector which corresponds to a prior probability over each possible action, in order to favor the selection of some over the others.
The value is directly backpropagated while the policy is used in the selection phase, where we slightly modify the UCT score's formula:
AlphaZero also introduces noise into the Monte Carlo tree search. Instead of using the raw policy output of the network, we add some noise (
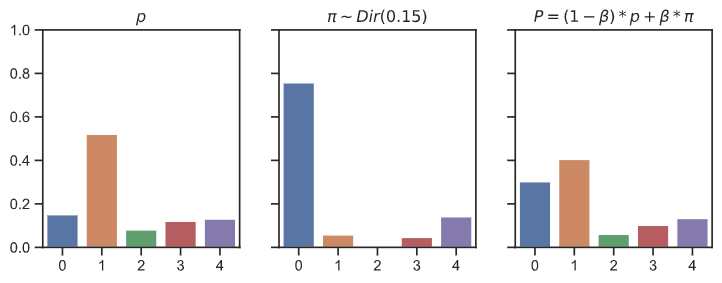
At early training stages, when the policy vector is more uniformly distributed, this ensures AlphaZero does sometimes play randomly and thus consider different types of game moves. While
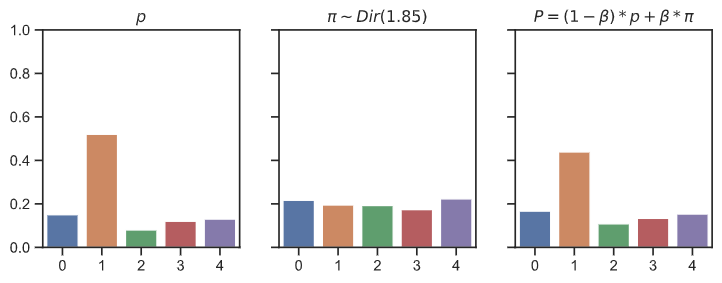
Finally, AlphaZero also adds a new temperature parameter
# Neural network
AlphaZero's neural network implements a deep residual architecture body and then splits into two distinct heads: one for the value and the other for the policy vector.
The body consists of a single convolutional block followed by 19 residual blocks. The convolutional block is composed by:
- A convolution of 256 filters of kernal size 3x3 with stride 1
- Batch normalization
- A rectifier nonlinearity
Each residual block is made of:
- A convolution of 256 filters of kernel size 3x3 with stride 1
- Batch normalization
- A rectifier nonlinearity
- A convolution of 256 filters of kernel size 3x3 with stride 1
- Batch normalization
- A skip connection that adds the input to the block
- A rectifier nonlinearity
The output of the residual tower is passed into the two separate value and policy heads. The policy head consists in:
- A convolution of 256 filters of kernel size 1x1 with stride 1
- Batch normalization
- A rectifier nonlinearity
- A fully connected linear layer
Finally, the value head contains:
- A convolution of 1 filter of kernel size 1x1 with stride 1
- Batch normalization
- A rectifier nonlinearity
- A fully connected linear layer to a hidden layer of size 256
- A rectifier nonlinearity
- A fully connected linear layer to a scalar
- A tanh nonlinearity outputting a scalar in the range
Here is the corresponding Keras code:
# Algorithm 2 - AlphaZero's neural network
from tensorflow.keras import layers, optimizers, regularizers, Input, Model
NUM_FILTERS = 256
NUM_BLOCKS = 19
CONV_SIZE = 3
REGULARIZATION = 0.0001
"""
Build a convolution layer.
@param input_data: input of the layer
@param filters: number of filters
@param conv_size: size of the convolution
@return: output of the convolution layer
"""
def conv_layer(input_data, filters, conv_size):
conv = layers.Conv2D(
filters=filters,
kernel_size=conv_size,
padding="same",
use_bias=False,
activation="linear",
kernel_regularizer=regularizers.l2(REGULARIZATION)
)(input_data)
conv = layers.BatchNormalization(axis=-1)(conv)
conv = layers.LeakyReLU()(conv)
return conv
"""
Build a residual block.
@param input_data: input of the block
@param filters: number of filters for the convolutions
@param conv_size: size of the convolutions
@return: output of the residual block
"""
def res_block(input_data, filters, conv_size):
res = conv_layer(input_data, filters, conv_size)
res = layers.Conv2D(
filters=filters,
kernel_size=conv_size,
padding="same",
use_bias=False,
activation="linear",
kernel_regularizer=regularizers.l2(REGULARIZATION)
)(res)
res = layers.BatchNormalization(axis=-1)(res)
res = layers.Add()([input_data, res])
res = layers.LeakyReLU()(res)
return res
input_data = Input(shape=(19, 19, 17))
# residual tower
x = conv_layer(input_data, NUM_FILTERS, CONV_SIZE)
for _ in range(NUM_BLOCKS):
x = res_block(x, NUM_FILTERS, CONV_SIZE)
# value head
value = conv_layer(x, 1, 1)
value = layers.Flatten()(value)
value = layers.Dense(
256, activation="linear", use_bias=False,
kernel_regularizer=regularizers.l2(REGULARIZATION)
)(value)
value = layers.LeakyReLU()(value)
value = layers.Dense(
1, activation="tanh", name="value", use_bias=False,
kernel_regularizer=regularizers.l2(REGULARIZATION)
)(value)
# policy head
policy = conv_layer(x, NUM_FILTERS, 1)
policy = layers.Flatten()(policy)
policy = layers.Dense(
# The board of the game of Go is 19x19, and we add a "pass" action
19*19 + 1, activation="softmax", name="policy", use_bias=False,
kernel_regularizer=regularizers.l2(REGULARIZATION)
)(policy)
# model
model = Model(input_data, [policy, value])
losses = {
"policy": "categorical_crossentropy",
"value": "mean_squared_error"
}
loss_weights = {
"policy": 0.5,
"value": 0.5
}
optimizer = optimizers.SGD(learning_rate=0.2, momentum=0.9, nesterov=True)
model.compile(optimizer=optimizer, loss=losses, loss_weights=loss_weights)
The policy head uses the categorical crossentropy loss, while the mean squared error is used for the value head. AlphaZero takes advantage of the Nesterov momentum in its Stochastic Gradient Descent (SGD) optimizer, using a momentum parameter of
# Learning process
AlphaZero learns by self-play, this means that it plays against itself and learns from that experience to play better. It uses a policy iteration algorithm: the more it trains, the more its actions near an ending state becomes accurate, and thus it can learn to be precise even sooner in the game thanks to the stronger value and policy signals. Moreover, its neural network is able to learn game patterns that can also be useful in early training stages.
More concretely, the training pipeline of AlphaZero consists in 3 stages, executed in parallel:
- Self-play: create a training set by recording games of the AlphaZero agent playing against himself. For each game state, we store: the representation of the game state, the policy vector from the Monte Carlo tree search and the winner (+1 if this player won, -1 if the other player won, 0 in case of a draw).
- Retrain network: sample a mini-batch of 2048 game states from the last 500k games and retrain the current neural network on these inputs.
- Evaluate network: after every 1000 training loops, test the new network to see if it is stronger. Play 400 games between the latest and the current best neural network. The latest neural network must at least win 55% of the games to be declared the new best player.
# Environment
Squadro is a 2 player board game edited by Gigamic [7]. The goal of the game is to move four of your five pawns across and back the board. During its turn, a player can move one of his pawns by the number of tiles indicated by the last checkpoint it passed. If his pawn reaches the other side of the board (a checkpoint), it stops and heads to the other side. If one or multiple enemy pawns cross its path, your pawn jumps over it/them and stop right after. The enemy pawn(s) go back to their last checkpoint.
Here is an example of Squadro game board:

Even if the rules are simple, Squadro is a complex game to master, even for computers. One aspect that makes it difficult is that it contains infinite loops, which seemed very counterintuitive to me. I was able to reproduce this behavior with an alpha-beta pruning agent whose goal is to maximize the opponent's distance to a goal state. Here is one example of an infinite loop:
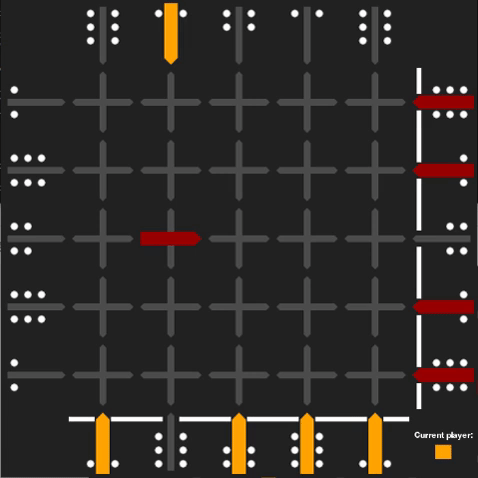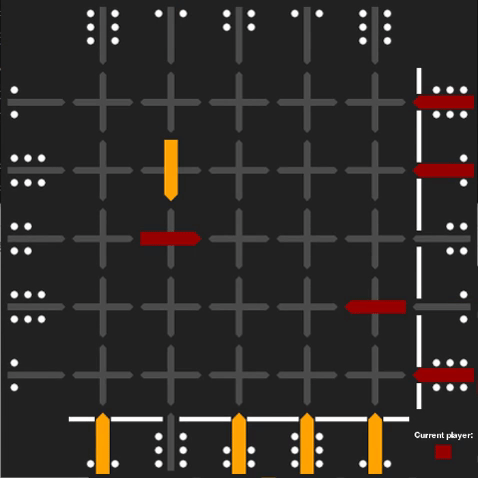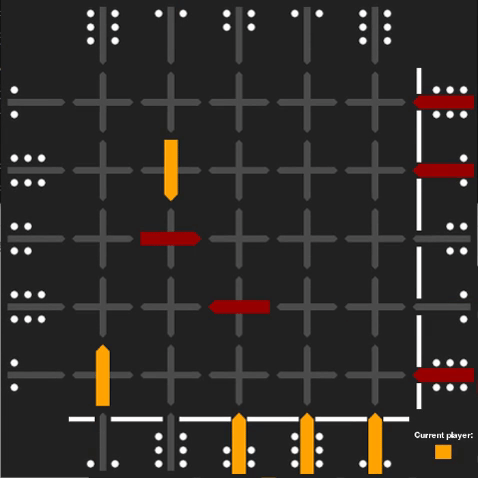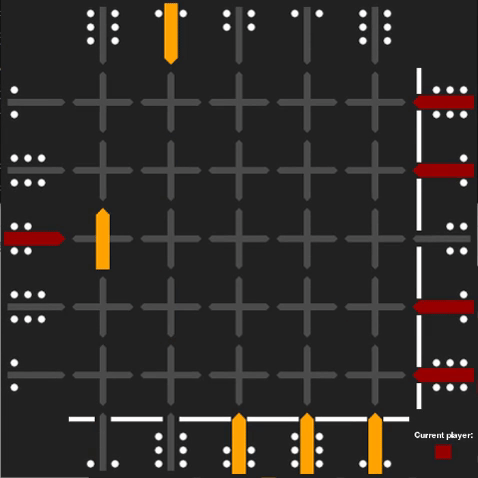
What makes Squadro interesting to work on is that it is not solvable by a deterministic algorithm. With a random player, Squadro's average number of turns is 70. Thus, we can compute an upper-bound for the number of nodes in the search tree for an average game:
# Challenges
# Computing resources
My implementation of AlphaZero was trained on a single laptop with no GPU at first, and then on a dedicated server (still no GPU - Intel Xeon E3-1230v6 - 4c/8t - 3.5GHz) for convenience. In practice, one should not train a (large) neural network on a CPU. I added this constraint to prove that AlphaZero can be used by anybody, even with a cheap non-distributed setup.
# Performance
Performance plays a critical role in the success of an implementation, even more in a non-distributed setting. I initially created my version of AlphaZero in Python before realizing memory management was a big issue. It now consists of a client (C++) and a server (Python). The client handles all the logic of the algorithm while the server corresponds to the neural network inference (implemented using TensorFlow). They communicate over gRPC [8]. Now, the bottleneck is the inference of the neural network: my CPU roughly takes 70ms to make a prediction for a batch size of 16 with a residual tower of 10 blocks with 128 filters. Proportionally, the computation time of the Monte Carlo tree search is practically neglectable. To improve the inference time, one could use a GPU and use a quantized version of the neural network (using for example, TensorRT [9]).
Because I am using a single computer, the 3-stages learning process is done sequentially instead of in parallel. In a more distributed setting, we may want to use a specific framework for handling the complexity of the communication between workers. Ray [10] seems to be a great candidate for that purpose.
To generate games more rapidly, the biggest improvement consists in using the parallel version of the Monte Carlo search tree: create a small batch of game states to be evaluated by the neural network, but each time you add a game state to the batch, temporarily consider it to be a loss (called a "virtual loss", this will prevent your search to always go down the same path). Then, evaluate your small batch, apply backpropagation and remove the virtual losses.
# Parameters tuning
The learning phase is the most time-consuming part by far. Indeed, AlphaZero contains many hyperparameters, and tuning them requires to restart the learning phase every time. With a single computer, we cannot easily sweep over all sets of parameters. For this reason, one should keep all the parameters to the defaults as explained in the original paper, and only tweak some of them.
# Monte Carlo tree search
Exploration parameter (
Number of rollouts (
Amount of Dirichlet noise (
# Neural network
Number of residual blocks (
Number of convolutional filters (
L2 regularization (
Learning rate (
Number of epochs (
# Learning process
Mini-batch size (
Number of games per training iteration (
Number of iterations before evaluation (
Size of the replay buffer (
Number of evaluation games (
# Results
In this section, I describe the performance of three AlphaZero agents:
- a small model: 5 residual blocks, 64 filters
- an intermediate model: 10 residual blocks, 128 filters
- a big model: 20 residual blocks, 256 filters
These three agents use the methods and parameters described earlier. They compete against two baseline agents:
- a human agent
- an alpha-beta pruning agent: its heuristic function was carefully crafted using multiple features. It is given 15 minutes for the entire game: in general, this allows it to see 13 actions in advance. It plays better than the humans I have tested it against (including myself).
Here are the results of the AlphaZero agents playing against the baselines:
| ref \ opponent (W/D/L) | human | alpha-beta |
|---|---|---|
| small (5x64) | 8/0/2 | 4/4/2 |
| intermediate (10x128) | 22/0/3 | 16/0/9 |
| big (20x256) | 50/0/0 | 50/0/0 |
The small model is of course the easiest to defeat. Indeed, its mid/late game looks invincible, but it may sometimes play inaccurately at the beginning of a game. I initially thought that it was due to the fact that I trained it with too few iterations, but it was not able to pass any more evaluation round. It was a great agent to experiment the different parameters of AlphaZero, but it is obviously way too small to reach superhuman performance.
The interpretation for the intermediate model is mostly similar to the small model: its early game is sometimes still too weak. One way to leverage this issue is to increase the number of rollouts, it takes more time to play but it looks much more accurate against a human. However, moderately increasing the number of rollouts does not impact its winrate against the alpha-beta agent.
Finally, the big model reaches our expectations: a 100% winrate against both baseline agents. It plays in a very aggressive way: for example, in game 2 of the Appendix, it has already finished 3 of its pawns on the 61th turn (for a total of 91 turns), while the human player did not finish any. It is generally a bad idea to finish that much pawns that early in a game, because having more pawns than the opponent gives more control on its pawns, and thus you are more likely to "steal" the win.
The following figure shows the confidence of AlphaZero (20x256, playing red) during game 1 of the Appendix. It also highlight two moments in the game, turns 30 and 70:
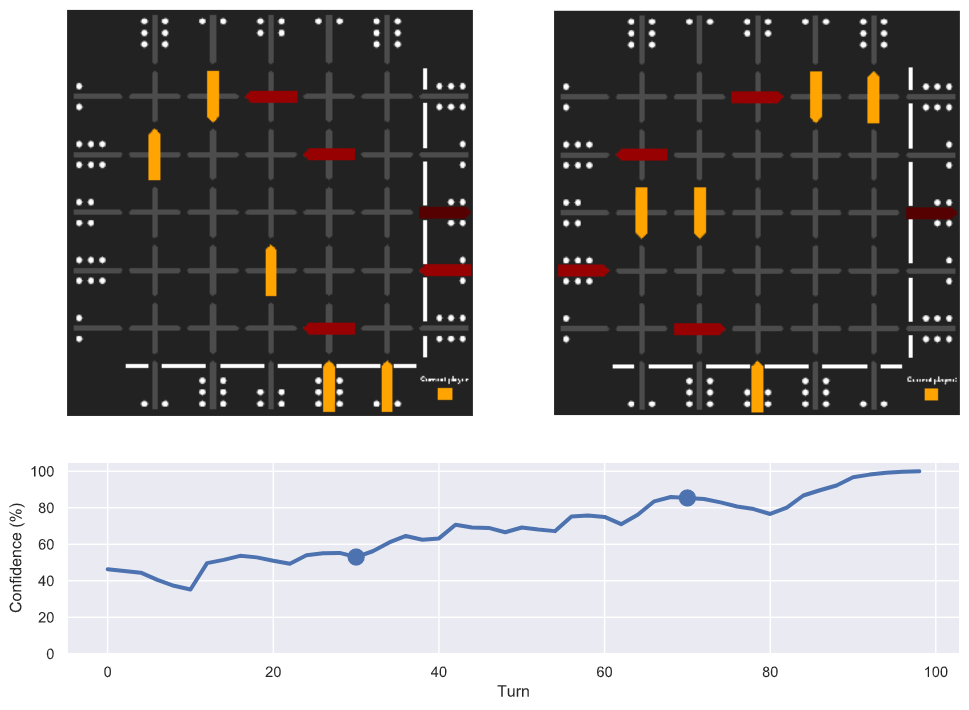
The first moment shows a fairly typical start: both agents did not make much progress and both have their pawns with a move step of 1 still under control. However, AlphaZero already decided to finish its middle pawn which would not be something a human player would do. Its confidence is only at
The second moment is also interesting and shows AlphaZero has a higher confidence (
# Conclusion
AlphaZero is a general reinforcement learning algorithm that performs great on many different games. As Deepmind have shown, it is able to play better than human professionals in complex games like Go, chess or shōgi using sound computing resources. In my work, I explained how the algorithm exactly works, I deeply discussed the usage of each hyper-parameter and finally, I showcased its performance on a moderately complex board game, Squadro, using a single computer with no GPU. This highlights the fact that AlphaZero is accessible to, literally, everyone. Reinforcement learning is an amazing domain to work in and I cannot wait to see how it will evolve in the coming years!
# References
- AlphaGo Zero: Starting from scratch. https://deepmind.com/blog/article/alphago-zero-starting-scratch
- AlphaZero: Shedding new light on chess, shogi, and Go. https://deepmind.com/blog/article/alphazero-shedding-new-light-grand-games-chess-shogi-and-go
- ELF: a platform for game research with AlphaGoZero/AlphaZero reimplementation. https://github.com/pytorch/ELF
- Leela Zero: Go engine with no human-provided knowledge, modeled after the AlphaGo Zero paper. https://github.com/leela-zero/leela-zero
- KataGo: GTP engine and self-play learning in Go. https://github.com/lightvector/KataGo
- AZFour: Connect Four powered by the AlphaZero Algorithm. https://azfour.com
- Squadro. https://www.gigamic.com/jeu/squadro-classic
- gRPC: A high-performance, open source universal RPC framework. https://grpc.io/
- TensorRT: TensorRT is a C++ library for high performance inference on NVIDIA GPUs and deep learning accelerators. https://github.com/NVIDIA/TensorRT
- Ray: A fast and simple framework for building and running distributed applications. Ray is packaged with RLlib, a scalable reinforcement learning library, and Tune, a scalable hyperparameter tuning library. https://github.com/ray-project/ray
# Appendix
# Examples of games
# Game 1
Player 0: alpha-beta
Player 1: AlphaZero (20x256)
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0
|_|_|_|_|_|_|<|1 |_|_|_|_|_|_|<|1 |_|_|_|_|_|<|_|1 |_|_|_|_|_|<|_|1 |_|_|_|_|<|_|_|1
|_|_|_|_|_|_|<|2 |_|_|_|_|_|_|<|2 |_|_|_|_|_|_|<|2 |_|_|_|_|_|_|<|2 |_|_|_|_|_|_|<|2
|_|_|_|_|_|_|<|3 |_|_|_|_|_|_|<|3 |_|_|_|_|_|_|<|3 |_|^|_|_|_|_|<|3 |_|^|_|_|_|_|<|3
|_|_|_|_|_|_|<|4 |_|^|_|_|_|_|<|4 |_|^|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4
|_|^|^|^|^|^|_| |_|_|^|^|^|^|_| |_|_|^|^|^|^|_| |_|_|^|^|^|^|_| |_|_|^|^|^|^|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0
|_|_|_|_|<|_|_|1 |_|_|_|<|_|_|_|1 |_|_|_|<|_|_|_|1 |_|_|<|_|_|_|_|1 |_|_|<|_|_|_|_|1
|_|^|_|_|_|_|<|2 |_|^|_|_|_|_|<|2 |_|^|_|_|_|_|<|2 |_|^|_|_|_|_|<|2 |_|^|^|_|_|_|<|2
|_|_|_|_|_|_|<|3 |_|_|_|_|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3
|_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4
|_|_|^|^|^|^|_| |_|_|^|^|^|^|_| |_|_|^|_|^|^|_| |_|_|^|_|^|^|_| |_|_|_|_|^|^|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|v|_|_|_|_| |_|_|v|_|_|_|_|
|_|_|_|_|_|_|<|0 |_|_|^|_|_|_|<|0 |_|_|^|_|_|_|<|0 |_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0
|_|_|<|_|_|_|_|1 |_|_|_|_|_|_|<|1 |_|_|_|_|_|_|<|1 |_|_|_|_|_|_|<|1 |_|_|_|_|_|_|<|1
|_|^|^|_|<|_|_|2 |_|^|_|_|<|_|_|2 |_|^|<|_|_|_|_|2 |_|^|<|_|_|_|_|2 |>|_|_|_|_|_|_|2
|_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3
|_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4
|_|_|_|_|^|^|_| |_|_|_|_|^|^|_| |_|_|_|_|^|^|_| |_|_|_|_|^|^|_| |_|^|_|_|^|^|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|v|_|_|_|_| |_|_|v|_|_|_|_| |_|_|v|_|_|_|_| |_|_|v|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0 |_|_|v|_|_|_|<|0
|_|_|_|_|_|_|<|1 |_|_|_|_|_|<|_|1 |_|_|_|_|_|<|_|1 |_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1
|>|_|_|_|_|_|_|2 |>|_|_|_|_|_|_|2 |>|_|_|_|_|_|_|2 |>|_|_|_|_|_|_|2 |>|_|_|_|_|_|_|2
|_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|^|_|^|_|_|<|3 |_|^|_|^|_|_|<|3 |_|^|_|^|_|_|<|3
|_|^|_|_|_|_|<|4 |_|^|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4
|_|_|_|_|^|^|_| |_|_|_|_|^|^|_| |_|_|_|_|^|^|_| |_|_|_|_|^|^|_| |_|_|_|_|^|^|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|v|_|_|_|<|0 |_|_|v|_|_|_|<|0 |_|_|v|_|_|_|<|0 |_|_|v|_|_|_|<|0 |_|_|v|_|_|_|<|0
|_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1
|>|_|_|_|_|_|_|2 |>|_|_|_|_|_|_|2 |>|_|_|_|_|_|_|2 |>|_|_|_|_|_|_|2 |_|_|>|_|_|_|_|2
|_|^|_|^|_|<|_|3 |_|^|_|^|_|<|_|3 |_|^|_|^|_|<|_|3 |_|^|_|^|_|<|_|3 |_|^|_|^|_|<|_|3
|_|_|_|_|_|_|<|4 |_|_|_|_|_|^|<|4 |_|_|_|_|<|_|_|4 |_|_|_|_|<|^|_|4 |_|_|_|_|<|^|_|4
|_|_|_|_|^|^|_| |_|_|_|_|^|_|_| |_|_|_|_|^|^|_| |_|_|_|_|^|_|_| |_|_|_|_|^|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|v|_|_|_|<|0 |_|_|v|_|_|_|<|0 |_|_|v|_|_|_|<|0 |_|_|v|_|_|_|<|0 |_|_|v|_|_|_|<|0
|_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1 |_|^|_|_|<|_|_|1
|_|_|>|_|_|^|_|2 |_|_|_|_|>|^|_|2 |_|^|_|_|>|^|_|2 |_|^|_|_|_|_|>|2 |_|_|_|_|_|_|>|2
|_|^|_|^|_|_|<|3 |_|^|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3
|_|_|_|_|<|_|_|4 |_|_|_|_|<|_|_|4 |_|_|_|_|<|_|_|4 |_|_|_|_|<|_|_|4 |_|_|_|_|<|_|_|4
|_|_|_|_|^|_|_| |_|_|_|_|^|_|_| |_|_|_|_|^|_|_| |_|_|_|_|^|^|_| |_|_|_|_|^|^|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|v|<|_|_|_|0 |_|_|v|<|_|_|_|0 |_|_|v|<|_|_|_|0 |_|_|_|<|_|_|_|0 |_|_|_|<|_|_|_|0
|_|^|_|_|<|_|_|1 |_|^|_|_|<|_|_|1 |_|^|_|_|<|_|_|1 |_|^|v|_|<|_|_|1 |_|^|v|_|<|_|_|1
|_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2
|_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3
|_|_|_|_|<|_|_|4 |_|_|_|_|<|^|_|4 |_|<|_|_|_|^|_|4 |_|<|_|_|_|^|_|4 |>|_|_|_|_|^|_|4
|_|_|_|_|^|^|_| |_|_|_|_|^|_|_| |_|_|_|_|^|_|_| |_|_|_|_|^|_|_| |_|_|_|_|^|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|_|<|_|_|_|0 |_|_|_|<|_|_|_|0 |_|^|_|<|_|_|_|0 |>|_|_|_|_|_|_|0 |>|_|_|_|_|_|_|0
|_|^|_|_|<|_|_|1 |_|^|_|_|<|_|_|1 |_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1
|_|_|v|_|_|_|>|2 |_|_|v|_|_|_|>|2 |_|_|v|_|_|_|>|2 |_|_|v|_|_|_|>|2 |_|_|v|_|_|_|>|2
|_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|^|_|^|_|_|<|3
|>|_|_|_|_|^|_|4 |_|>|_|_|_|^|_|4 |_|>|_|_|_|^|_|4 |_|>|_|_|_|^|_|4 |>|_|_|_|_|^|_|4
|_|_|_|_|^|_|_| |_|_|_|_|^|_|_| |_|_|_|_|^|_|_| |_|^|_|_|^|_|_| |_|_|_|_|^|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|>|_|_|_|_|_|0 |_|>|_|_|_|_|_|0 |_|_|>|_|_|_|_|0 |_|_|>|_|_|_|_|0 |_|_|>|_|_|_|_|0
|_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1
|_|_|v|_|_|_|>|2 |_|^|v|_|_|_|>|2 |_|^|v|_|_|_|>|2 |_|^|v|_|_|_|>|2 |_|^|v|_|_|_|>|2
|_|^|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|^|<|3 |_|_|_|^|<|_|_|3
|>|_|_|_|_|^|_|4 |>|_|_|_|_|^|_|4 |>|_|_|_|_|^|_|4 |>|_|_|_|_|_|_|4 |>|_|_|_|_|_|_|4
|_|_|_|_|^|_|_| |_|_|_|_|^|_|_| |_|_|_|_|^|_|_| |_|_|_|_|^|_|_| |_|_|_|_|^|^|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|>|_|_|_|_|0 |_|_|>|_|_|_|_|0 |_|_|>|_|^|_|_|0 |_|_|>|_|^|_|_|0 |_|_|>|_|^|_|_|0
|_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1 |_|_|_|_|_|_|<|1 |_|_|_|_|_|<|_|1 |_|_|_|_|_|<|_|1
|_|^|v|_|^|_|>|2 |_|^|v|_|^|_|>|2 |_|^|v|_|_|_|>|2 |_|^|v|_|_|_|>|2 |_|^|v|_|_|_|>|2
|_|_|_|^|_|_|<|3 |_|_|_|^|_|<|_|3 |_|_|_|^|_|<|_|3 |_|_|_|^|_|<|_|3 |_|_|_|^|_|<|_|3
|>|_|_|_|_|_|_|4 |>|_|_|_|_|_|_|4 |>|_|_|_|_|_|_|4 |>|_|_|_|_|_|_|4 |>|_|_|_|_|^|_|4
|_|_|_|_|_|^|_| |_|_|_|_|_|^|_| |_|_|_|_|_|^|_| |_|_|_|_|_|^|_| |_|_|_|_|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|>|_|^|_|_|0 |_|_|>|_|^|_|_|0 |_|_|>|_|^|_|_|0 |_|_|>|_|^|_|_|0 |_|_|>|_|^|_|_|0
|_|_|_|_|_|<|_|1 |_|_|_|_|_|<|_|1 |_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1
|_|^|v|_|_|_|>|2 |_|^|v|_|_|_|>|2 |_|^|v|_|_|_|>|2 |_|^|v|_|_|^|>|2 |_|^|v|_|_|^|>|2
|_|_|_|^|<|_|_|3 |_|_|_|^|<|^|_|3 |_|_|_|^|<|^|_|3 |_|_|_|^|<|_|_|3 |_|_|_|^|<|_|_|3
|>|_|_|_|_|^|_|4 |>|_|_|_|_|_|_|4 |>|_|_|_|_|_|_|4 |>|_|_|_|_|_|_|4 |_|>|_|_|_|_|_|4
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|v|_|_|_|_|_|
|_|_|>|_|^|_|_|0 |_|_|>|_|^|_|_|0 |_|^|>|_|^|_|_|0 |_|^|>|_|^|_|_|0 |_|_|>|_|^|_|_|0
|_|^|_|_|<|_|_|1 |_|^|_|_|<|_|_|1 |_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1
|_|_|v|_|_|^|>|2 |_|_|v|_|_|^|>|2 |_|_|v|_|_|^|>|2 |_|_|v|_|_|^|>|2 |_|_|v|_|_|^|>|2
|_|_|_|^|<|_|_|3 |_|_|<|_|_|_|_|3 |_|_|<|_|_|_|_|3 |_|<|_|_|_|_|_|3 |_|<|_|_|_|_|_|3
|_|>|_|_|_|_|_|4 |_|>|_|_|_|_|_|4 |_|>|_|_|_|_|_|4 |_|>|_|_|_|_|_|4 |_|>|_|_|_|_|_|4
|_|_|_|_|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|v|_|_|_|_|_| |_|v|_|_|v|_|_| |_|v|_|_|v|_|_| |_|v|_|_|v|_|_| |_|v|_|_|v|_|_|
|_|_|>|_|^|_|_|0 |_|_|>|_|_|_|_|0 |_|_|>|_|_|_|_|0 |_|_|>|_|_|_|_|0 |_|_|>|_|_|_|_|0
|_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1 |_|_|_|<|_|_|_|1 |_|_|_|<|_|^|_|1 |_|_|_|<|_|^|_|1
|_|_|v|_|_|^|>|2 |_|_|v|_|_|^|>|2 |_|_|v|_|_|^|>|2 |_|_|v|_|_|_|>|2 |_|_|v|_|_|_|>|2
|>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3
|_|>|_|_|_|_|_|4 |_|>|_|_|_|_|_|4 |_|>|_|_|_|_|_|4 |_|>|_|_|_|_|_|4 |_|_|>|_|_|_|_|4
|_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|v|_|_| |_|_|_|_|v|_|_| |_|_|_|_|v|_|_| |_|_|_|_|v|_|_| |_|_|_|_|_|_|_|
|_|_|>|_|_|_|_|0 |_|_|>|_|_|_|_|0 |_|_|>|_|_|^|_|0 |_|_|>|_|_|^|_|0 |_|_|>|_|v|^|_|0
|_|_|_|<|_|^|_|1 |_|_|<|_|_|^|_|1 |_|_|<|_|_|_|_|1 |_|<|_|_|_|_|_|1 |_|<|_|_|_|_|_|1
|_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2
|>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3
|_|_|>|_|_|_|_|4 |_|_|>|_|_|_|_|4 |_|_|>|_|_|_|_|4 |_|_|>|_|_|_|_|4 |_|_|>|_|_|_|_|4
|_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_|
|_|_|_|>|v|^|_|0 |_|_|_|>|_|^|_|0 |_|_|_|_|>|^|_|0 |_|_|_|_|>|_|_|0 |_|_|_|_|>|_|_|0
|_|<|_|_|_|_|_|1 |_|<|_|_|v|_|_|1 |_|<|_|_|v|_|_|1 |_|<|_|_|v|_|_|1 |>|_|_|_|v|_|_|1
|_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2
|>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3
|_|_|>|_|_|_|_|4 |_|_|>|_|_|_|_|4 |_|_|>|_|_|_|_|4 |_|_|>|_|_|_|_|4 |_|_|>|_|_|_|_|4
|_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_|
|_|_|_|_|>|_|_|0 |_|_|_|_|>|_|_|0 |_|_|_|_|>|_|_|0 |_|_|_|_|>|_|_|0 |_|_|_|_|>|_|_|0
|>|_|_|_|_|_|_|1 |_|_|_|>|_|_|_|1 |_|_|_|>|_|_|_|1 |_|_|_|>|_|_|_|1 |_|_|_|>|_|_|_|1
|_|v|v|_|v|_|>|2 |_|v|v|_|v|_|>|2 |_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2
|>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3 |>|_|_|_|v|_|_|3 |>|_|_|_|v|_|_|3 |>|_|_|^|v|_|_|3
|_|_|>|_|_|_|_|4 |_|_|>|_|_|_|_|4 |_|_|>|_|_|_|_|4 |_|_|_|>|_|_|_|4 |>|_|_|_|_|_|_|4
|_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|_|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|v|_| |_|_|_|_|_|_|_| |_|_|_|_|v|_|_| |_|_|_|_|v|_|_| |_|_|_|_|v|_|_|
|_|_|_|_|_|>|_|0 |>|_|_|_|_|_|_|0 |>|_|_|_|_|_|_|0 |>|_|_|_|_|_|_|0 |>|_|_|_|_|_|_|0
|_|_|_|>|_|_|_|1 |_|_|_|>|_|v|_|1 |_|_|_|>|_|v|_|1 |_|_|_|>|_|_|_|1 |_|_|_|_|_|_|>|1
|_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2
|>|_|_|^|v|_|_|3 |>|_|_|^|v|_|_|3 |_|_|_|_|_|>|_|3 |>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3
|>|_|_|_|_|_|_|4 |>|_|_|_|_|_|_|4 |>|_|_|_|_|_|_|4 |>|_|_|_|_|v|_|4 |>|_|_|_|_|v|_|4
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|>|_|_|_|v|_|_|0 |_|>|_|_|v|_|_|0 |_|>|_|_|_|_|_|0 |_|_|>|_|_|_|_|0 |_|_|>|_|_|_|_|0
|_|_|_|_|_|_|>|1 |_|_|_|_|_|_|>|1 |_|_|_|_|v|_|>|1 |_|_|_|_|v|_|>|1 |_|_|_|_|_|_|>|1
|_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2 |_|v|v|_|v|_|>|2
|>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3
|>|_|_|_|_|v|_|4 |>|_|_|_|_|v|_|4 |>|_|_|_|_|v|_|4 |>|_|_|_|_|v|_|4 |>|_|_|_|_|v|_|4
|_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|_|>|_|_|_|0 |_|_|_|>|_|_|_|0 |_|_|_|_|>|_|_|0 |_|_|_|_|>|_|_|0 |_|_|_|_|_|>|_|0
|_|_|_|_|_|_|>|1 |_|_|_|_|_|_|>|1 |_|_|_|_|_|_|>|1 |_|_|_|^|_|_|>|1 |_|_|_|^|_|_|>|1
|_|v|v|_|v|_|>|2 |_|v|v|_|v|_|>|2 |_|v|v|_|v|_|>|2 |_|v|v|_|v|_|>|2 |_|v|v|_|v|_|>|2
|>|_|_|_|_|_|_|3 |>|_|_|^|_|_|_|3 |>|_|_|^|_|_|_|3 |>|_|_|_|_|_|_|3 |>|_|_|_|_|_|_|3
|>|_|_|_|_|v|_|4 |>|_|_|_|_|v|_|4 |>|_|_|_|_|v|_|4 |>|_|_|_|_|v|_|4 |>|_|_|_|_|v|_|4
|_|_|_|^|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|_|_|_|>|_|0 |_|_|_|_|_|>|_|0 |_|_|_|_|_|>|_|0 |_|_|_|_|_|>|_|0 |_|_|_|_|_|>|_|0
|_|_|_|^|_|_|>|1 |_|_|_|^|_|_|>|1 |_|_|_|^|_|_|>|1 |_|_|_|^|_|_|>|1 |_|_|_|^|_|_|>|1
|_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2 |_|v|v|_|_|_|>|2
|>|_|_|_|v|_|_|3 |_|_|_|>|v|_|_|3 |_|_|_|>|_|_|_|3 |_|_|_|_|_|_|>|3 |_|_|_|_|_|_|>|3
|>|_|_|_|_|v|_|4 |>|_|_|_|_|v|_|4 |>|_|_|_|v|v|_|4 |>|_|_|_|v|v|_|4 |>|_|_|_|_|v|_|4
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|v|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _
|_|_|_|_|_|_|_|
|_|_|_|_|_|_|>|0
|_|_|_|^|_|_|>|1
|_|v|v|_|_|_|>|2
|_|_|_|_|_|_|>|3
|>|_|_|_|_|v|_|4
|_|_|_|_|v|_|_|
0 1 2 3 4
# Game 2
Player 0: human
Player 1: AlphaZero (20x256)
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0
|_|_|_|_|_|_|<|1 |_|_|_|_|_|_|<|1 |_|_|_|_|_|<|_|1 |_|_|_|_|_|<|_|1 |_|_|_|_|_|<|_|1
|_|_|_|_|_|_|<|2 |_|_|_|_|_|_|<|2 |_|_|_|_|_|_|<|2 |_|_|_|_|_|_|<|2 |_|_|_|_|_|_|<|2
|_|_|_|_|_|_|<|3 |_|_|_|_|_|_|<|3 |_|_|_|_|_|_|<|3 |_|_|_|_|_|_|<|3 |_|_|_|_|_|_|<|3
|_|_|_|_|_|_|<|4 |_|_|_|_|_|^|<|4 |_|_|_|_|_|^|<|4 |_|^|_|_|_|^|<|4 |_|^|_|_|<|_|_|4
|_|^|^|^|^|^|_| |_|^|^|^|^|_|_| |_|^|^|^|^|_|_| |_|_|^|^|^|_|_| |_|_|^|^|^|^|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0
|_|_|_|_|_|<|_|1 |_|_|_|_|_|<|_|1 |_|_|_|_|_|<|_|1 |_|_|_|_|<|_|_|1 |_|_|_|_|<|_|_|1
|_|_|_|_|_|_|<|2 |_|_|_|_|<|_|_|2 |_|^|_|_|<|_|_|2 |_|^|_|_|<|_|_|2 |_|^|_|_|<|_|_|2
|_|^|_|_|_|_|<|3 |_|^|_|_|_|_|<|3 |_|_|_|_|_|_|<|3 |_|_|_|_|_|_|<|3 |_|_|_|_|^|_|<|3
|_|_|_|_|<|_|_|4 |_|_|_|_|<|_|_|4 |_|_|_|_|<|_|_|4 |_|_|_|_|<|_|_|4 |_|_|_|_|_|_|<|4
|_|_|^|^|^|^|_| |_|_|^|^|^|^|_| |_|_|^|^|^|^|_| |_|_|^|^|^|^|_| |_|_|^|^|_|^|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|_|_|_|_|<|0 |_|_|_|_|_|_|<|0 |_|_|_|<|_|_|_|0 |_|_|_|<|_|_|_|0 |_|_|_|<|_|_|_|0
|_|_|_|<|_|_|_|1 |_|^|_|<|_|_|_|1 |_|^|_|<|_|_|_|1 |_|^|_|<|_|_|_|1 |_|^|_|<|_|_|_|1
|_|^|_|_|<|_|_|2 |_|_|_|_|<|_|_|2 |_|_|_|_|<|_|_|2 |_|_|^|_|<|_|_|2 |_|<|_|_|_|_|_|2
|_|_|_|_|^|_|<|3 |_|_|_|_|^|_|<|3 |_|_|_|_|^|_|<|3 |_|_|_|_|^|_|<|3 |_|_|_|_|^|_|<|3
|_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4
|_|_|^|^|_|^|_| |_|_|^|^|_|^|_| |_|_|^|^|_|^|_| |_|_|_|^|_|^|_| |_|_|^|^|_|^|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|_|<|_|_|_|0 |_|_|_|<|_|_|_|0 |_|_|_|<|_|_|_|0 |_|_|_|<|_|_|_|0 |_|_|_|<|_|_|_|0
|_|^|_|<|_|_|_|1 |_|^|_|<|_|_|_|1 |_|^|_|<|_|_|_|1 |_|^|_|<|_|_|_|1 |_|^|_|<|_|_|_|1
|_|<|^|_|_|_|_|2 |_|<|^|_|_|_|_|2 |_|<|^|_|_|_|_|2 |>|_|^|_|_|_|_|2 |>|_|^|_|_|^|_|2
|_|_|_|_|^|_|<|3 |_|_|_|_|^|<|_|3 |_|_|_|_|^|<|_|3 |_|_|_|_|^|<|_|3 |_|_|_|_|^|_|<|3
|_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|^|<|4 |_|_|_|_|_|^|<|4 |_|_|_|_|_|_|<|4
|_|_|_|^|_|^|_| |_|_|_|^|_|^|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|_|<|_|_|_|0 |_|_|_|<|_|_|_|0 |_|_|_|<|_|_|_|0 |_|_|_|<|_|_|_|0 |_|_|_|<|_|_|_|0
|_|^|_|<|_|_|_|1 |_|^|_|<|_|_|_|1 |_|^|<|_|_|_|_|1 |_|^|<|_|_|^|_|1 |>|_|_|_|_|^|_|1
|_|_|_|>|_|^|_|2 |_|_|_|>|_|^|_|2 |_|_|_|>|_|^|_|2 |_|_|_|>|_|_|_|2 |_|_|_|>|_|_|_|2
|_|_|_|_|^|_|<|3 |_|_|_|^|^|_|<|3 |_|_|_|^|^|_|<|3 |_|_|_|^|^|_|<|3 |_|_|_|^|^|_|<|3
|_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4
|_|_|^|^|_|_|_| |_|_|^|_|_|_|_| |_|_|^|_|_|_|_| |_|_|^|_|_|_|_| |_|^|^|_|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|v|_|
|_|_|_|<|^|_|_|0 |_|_|_|<|^|_|_|0 |_|_|_|<|^|^|_|0 |_|_|_|<|^|^|_|0 |_|_|_|<|^|_|_|0
|>|_|_|_|_|^|_|1 |>|_|_|_|_|^|_|1 |>|_|_|_|_|_|_|1 |>|_|_|_|_|_|_|1 |>|_|_|_|_|_|_|1
|_|_|_|>|_|_|_|2 |_|_|_|_|_|>|_|2 |_|_|_|_|_|>|_|2 |_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2
|_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3
|_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4
|_|^|^|_|_|_|_| |_|^|^|_|_|_|_| |_|^|^|_|_|_|_| |_|^|^|_|_|_|_| |_|^|^|_|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|v|v|_| |_|_|_|_|v|v|_|
|>|_|_|_|^|_|_|0 |>|_|_|_|^|_|_|0 |>|_|_|_|^|_|_|0 |>|_|_|_|_|_|_|0 |>|_|_|_|_|_|_|0
|>|_|_|_|_|_|_|1 |>|_|_|_|_|_|_|1 |>|_|_|_|_|_|_|1 |>|_|_|_|_|_|_|1 |>|_|_|_|_|_|_|1
|_|_|_|_|_|_|>|2 |_|_|^|_|_|_|>|2 |_|_|^|_|_|_|>|2 |_|_|^|_|_|_|>|2 |_|_|^|_|_|_|>|2
|_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|<|_|3 |_|_|_|^|_|<|_|3 |_|_|_|^|<|_|_|3
|_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4
|_|^|^|_|_|_|_| |_|^|_|_|_|_|_| |_|^|_|_|_|_|_| |_|^|_|_|_|_|_| |_|^|_|_|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|v|_|_|v|_|
|>|_|_|_|v|_|_|0 |>|_|_|_|v|_|_|0 |>|_|_|_|v|_|_|0 |>|_|_|_|v|_|_|0 |>|_|_|_|v|_|_|0
|>|_|_|_|_|_|_|1 |>|_|_|_|_|_|_|1 |>|_|_|_|_|_|_|1 |_|_|_|>|_|_|_|1 |_|_|_|>|_|_|_|1
|_|_|^|_|_|_|>|2 |_|_|^|_|_|_|>|2 |_|_|^|_|_|_|>|2 |_|_|^|_|_|_|>|2 |_|_|_|_|_|_|>|2
|_|_|_|^|<|_|_|3 |_|_|<|_|_|_|_|3 |_|_|<|_|_|_|_|3 |_|_|<|_|_|_|_|3 |_|_|<|_|_|_|_|3
|_|_|_|_|_|_|<|4 |_|_|_|_|_|_|<|4 |_|^|_|_|_|_|<|4 |_|^|_|_|_|_|<|4 |_|^|_|_|_|_|<|4
|_|^|_|_|_|_|_| |_|^|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|v|_|_|v|_| |_|_|v|_|_|v|_| |_|_|v|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_|
|>|_|_|_|v|_|_|0 |>|_|_|_|_|_|_|0 |>|_|_|_|_|_|_|0 |>|_|v|_|_|_|_|0 |>|_|v|_|_|_|_|0
|_|_|_|_|_|_|>|1 |_|_|_|_|v|_|>|1 |_|_|_|_|v|_|>|1 |_|_|_|_|v|_|>|1 |_|_|_|_|v|_|>|1
|_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2
|_|_|<|_|_|_|_|3 |_|_|<|_|_|_|_|3 |_|_|<|_|_|_|_|3 |_|_|<|_|_|_|_|3 |_|_|<|_|_|_|_|3
|_|^|_|_|_|_|<|4 |_|^|_|_|_|_|<|4 |_|^|_|<|_|_|_|4 |_|^|_|<|_|_|_|4 |>|_|_|_|_|_|_|4
|_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|^|_|^|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_|
|>|_|v|_|_|_|_|0 |>|_|v|_|_|_|_|0 |>|_|v|_|_|_|_|0 |_|>|v|_|_|_|_|0 |_|>|_|_|_|_|_|0
|_|_|_|_|v|_|>|1 |_|_|_|_|v|_|>|1 |_|_|_|_|v|_|>|1 |_|_|_|_|v|_|>|1 |_|_|v|_|v|_|>|1
|_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2
|_|_|<|_|_|_|_|3 |_|_|<|_|_|_|_|3 |_|_|<|_|_|_|_|3 |_|_|<|_|_|_|_|3 |_|_|<|_|_|_|_|3
|>|^|_|_|_|_|_|4 |_|_|>|_|_|_|_|4 |_|^|>|_|_|_|_|4 |_|^|>|_|_|_|_|4 |_|^|>|_|_|_|_|4
|_|_|_|^|_|_|_| |_|^|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_| |_|_|_|^|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_|
|_|>|_|_|_|_|_|0 |_|>|_|_|_|_|_|0 |_|>|_|_|_|_|_|0 |_|>|_|_|_|_|_|0 |_|>|_|_|_|_|_|0
|_|_|v|_|v|_|>|1 |_|_|v|_|v|_|>|1 |_|_|v|_|v|_|>|1 |_|_|v|_|v|_|>|1 |_|_|v|_|v|_|>|1
|_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2
|_|_|<|_|_|_|_|3 |_|_|<|^|_|_|_|3 |_|_|<|^|_|_|_|3 |_|_|<|^|_|_|_|3 |_|_|<|^|_|_|_|3
|_|^|_|>|_|_|_|4 |>|^|_|_|_|_|_|4 |_|_|>|_|_|_|_|4 |_|^|>|_|_|_|_|4 |_|^|_|>|_|_|_|4
|_|_|_|^|_|_|_| |_|_|_|_|_|_|_| |_|^|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_|
|_|>|_|_|_|_|_|0 |_|>|_|_|_|_|_|0 |_|>|_|_|_|_|_|0 |_|>|_|_|_|_|_|0 |_|>|_|_|_|_|_|0
|_|_|_|_|v|_|>|1 |_|_|_|_|v|_|>|1 |_|_|_|_|v|_|>|1 |_|_|_|_|v|_|>|1 |_|_|_|_|_|_|>|1
|_|_|v|_|_|_|>|2 |_|_|v|_|_|_|>|2 |_|_|_|_|_|_|>|2 |_|_|_|_|_|_|>|2 |_|_|_|_|v|_|>|2
|_|_|<|^|_|_|_|3 |_|_|<|^|_|_|_|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3
|_|^|_|>|_|_|_|4 |_|^|_|_|>|_|_|4 |_|^|v|_|>|_|_|4 |_|^|v|_|_|>|_|4 |_|^|v|_|_|>|_|4
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_|
|_|>|_|_|_|_|_|0 |_|>|_|_|_|_|_|0 |_|_|>|_|_|_|_|0 |_|_|>|_|_|_|_|0 |_|_|>|_|_|_|_|0
|_|_|_|_|_|_|>|1 |_|_|_|_|_|_|>|1 |_|_|_|_|_|_|>|1 |_|_|_|^|_|_|>|1 |_|_|_|^|_|_|>|1
|_|_|_|_|v|_|>|2 |_|_|_|_|v|_|>|2 |_|_|_|_|v|_|>|2 |_|_|_|_|v|_|>|2 |_|_|_|_|v|_|>|2
|_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|^|_|_|<|3 |_|_|_|_|_|_|<|3 |_|_|_|_|_|<|_|3
|_|^|v|_|_|_|>|4 |_|^|_|_|_|_|>|4 |_|^|_|_|_|_|>|4 |_|^|_|_|_|_|>|4 |_|^|_|_|_|_|>|4
|_|_|_|_|_|_|_| |_|_|v|_|_|_|_| |_|_|v|_|_|_|_| |_|_|v|_|_|_|_| |_|_|v|_|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|v|_|v|_| |_|_|_|v|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_|
|_|_|>|_|_|_|_|0 |_|_|_|>|_|_|_|0 |>|_|_|_|_|_|_|0 |_|>|_|_|_|_|_|0 |_|>|_|_|_|_|_|0
|_|_|_|_|_|_|>|1 |_|_|_|_|_|_|>|1 |_|_|_|v|_|_|>|1 |_|_|_|v|_|_|>|1 |_|_|_|_|_|_|>|1
|_|_|_|_|v|_|>|2 |_|_|_|_|v|_|>|2 |_|_|_|_|v|_|>|2 |_|_|_|_|v|_|>|2 |_|_|_|_|v|_|>|2
|_|_|_|_|_|<|_|3 |_|_|_|_|_|<|_|3 |_|_|_|_|_|<|_|3 |_|_|_|_|_|<|_|3 |_|_|_|v|_|<|_|3
|_|^|_|_|_|_|>|4 |_|^|_|_|_|_|>|4 |_|^|_|_|_|_|>|4 |_|^|_|_|_|_|>|4 |_|^|_|_|_|_|>|4
|_|_|v|_|_|_|_| |_|_|v|_|_|_|_| |_|_|v|_|_|_|_| |_|_|v|_|_|_|_| |_|_|v|_|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|v|_|
|_|_|>|_|_|_|_|0 |_|_|>|_|_|_|_|0 |_|_|_|>|_|_|_|0 |_|_|_|>|_|_|_|0 |_|_|_|_|>|_|_|0
|_|_|_|_|_|_|>|1 |_|_|_|_|_|_|>|1 |_|_|_|_|_|_|>|1 |_|_|_|_|_|_|>|1 |_|_|_|_|_|_|>|1
|_|_|_|_|v|_|>|2 |_|_|_|_|v|_|>|2 |_|_|_|_|v|_|>|2 |_|_|_|_|v|_|>|2 |_|_|_|_|v|_|>|2
|_|_|_|v|_|<|_|3 |_|_|_|_|_|<|_|3 |_|_|_|_|_|<|_|3 |_|^|_|_|_|<|_|3 |_|^|_|_|_|<|_|3
|_|^|_|_|_|_|>|4 |_|^|_|_|_|_|>|4 |_|^|_|_|_|_|>|4 |_|_|_|_|_|_|>|4 |_|_|_|_|_|_|>|4
|_|_|v|_|_|_|_| |_|_|v|v|_|_|_| |_|_|v|v|_|_|_| |_|_|v|v|_|_|_| |_|_|v|v|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|v|_| |_|_|_|_|_|v|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|_|_|>|_|_|0 |_|_|_|_|_|>|_|0 |>|_|_|_|_|_|_|0 |_|>|_|_|_|_|_|0 |_|>|_|_|_|_|_|0
|_|_|_|_|_|_|>|1 |_|_|_|_|_|_|>|1 |_|_|_|_|_|v|>|1 |_|_|_|_|_|v|>|1 |_|_|_|_|_|_|>|1
|_|^|_|_|v|_|>|2 |_|^|_|_|v|_|>|2 |_|^|_|_|v|_|>|2 |_|^|_|_|v|_|>|2 |_|^|_|_|v|_|>|2
|_|_|_|_|_|<|_|3 |_|_|_|_|_|<|_|3 |_|_|_|_|_|<|_|3 |_|_|_|_|_|<|_|3 |_|_|_|_|_|_|<|3
|_|_|_|_|_|_|>|4 |_|_|_|_|_|_|>|4 |_|_|_|_|_|_|>|4 |_|_|_|_|_|_|>|4 |_|_|_|_|_|v|>|4
|_|_|v|v|_|_|_| |_|_|v|v|_|_|_| |_|_|v|v|_|_|_| |_|_|v|v|_|_|_| |_|_|v|v|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|>|_|_|_|_|_|0 |_|>|_|_|_|_|_|0 |_|_|>|_|_|_|_|0 |_|^|>|_|_|_|_|0 |_|^|_|>|_|_|_|0
|_|_|_|_|_|_|>|1 |_|^|_|_|_|_|>|1 |_|^|_|_|_|_|>|1 |_|_|_|_|_|_|>|1 |_|_|_|_|_|_|>|1
|_|^|_|_|v|_|>|2 |_|_|_|_|v|_|>|2 |_|_|_|_|v|_|>|2 |_|_|_|_|v|_|>|2 |_|_|_|_|v|_|>|2
|_|_|_|_|_|<|_|3 |_|_|_|_|_|<|_|3 |_|_|_|_|_|<|_|3 |_|_|_|_|_|<|_|3 |_|_|_|_|_|<|_|3
|_|_|_|_|_|v|>|4 |_|_|_|_|_|v|>|4 |_|_|_|_|_|v|>|4 |_|_|_|_|_|v|>|4 |_|_|_|_|_|v|>|4
|_|_|v|v|_|_|_| |_|_|v|v|_|_|_| |_|_|v|v|_|_|_| |_|_|v|v|_|_|_| |_|_|v|v|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
|_|v|_|_|_|_|_| |_|v|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_| |_|_|_|_|_|_|_|
|_|_|_|>|_|_|_|0 |_|_|_|_|>|_|_|0 |_|_|_|_|>|_|_|0 |_|_|_|_|_|>|_|0 |_|_|_|_|_|>|_|0
|_|_|_|_|_|_|>|1 |_|_|_|_|_|_|>|1 |_|_|_|_|_|_|>|1 |_|_|_|_|_|_|>|1 |_|_|_|_|_|_|>|1
|_|_|_|_|v|_|>|2 |_|_|_|_|v|_|>|2 |_|v|_|_|v|_|>|2 |_|v|_|_|v|_|>|2 |_|_|_|_|v|_|>|2
|_|_|_|_|_|<|_|3 |_|_|_|_|_|<|_|3 |_|_|_|_|_|<|_|3 |_|_|_|_|_|<|_|3 |_|_|_|_|_|<|_|3
|_|_|_|_|_|v|>|4 |_|_|_|_|_|v|>|4 |_|_|_|_|_|v|>|4 |_|_|_|_|_|v|>|4 |_|_|_|_|_|v|>|4
|_|_|v|v|_|_|_| |_|_|v|v|_|_|_| |_|_|v|v|_|_|_| |_|_|v|v|_|_|_| |_|v|v|v|_|_|_|
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
_ _ _ _ _ _ _
|_|_|_|_|_|_|_|
|_|_|_|_|_|_|>|0
|_|_|_|_|_|_|>|1
|_|_|_|_|v|_|>|2
|_|_|_|_|_|<|_|3
|_|_|_|_|_|v|>|4
|_|v|v|v|_|_|_|
0 1 2 3 4